
In particular, the chi-square distribution will arise in the study of the sample variance when the underlying distribution is normal and in goodness of fit tests. For example, if you're interested in either a cumulative probability of 0.60, or an upper probability of 0.40, you'll want to look for the \(t\)-value in the first column. Kyle Siegrist University of Alabama in Huntsville via Random Services In this section we will study a distribution, and some relatives, that have special importance in statistics. Example: Reporting a chi-square test There was no significant relationship between handedness and nationality, 2 (1, N 428) 0.44, p. The row shaded in green indicates the upper \(\alpha\) probability that corresponds to the \(1-\alpha\) cumulative probability. Report the chi-square alongside its degrees of freedom, sample size, and p value, following this format: 2 (degrees of freedom, N sample size) chi-square value, p p value). The \(t\)-table is similar to the chi-square table in that the inside of the \(t\)-table (shaded in purple) contains the \(t\)-values for various cumulative probabilities (shaded in red), such as 0.60, 0.75, 0.90, 0.95, 0.975, 0.99, and 0.995, and for various \(t\) distributions with \(r\) degrees of freedom (shaded in blue). The chi-square distribution is used for inference concerning observations drawn from an exponential population and in determining the critical values for the chi-square goodness-of-t test.
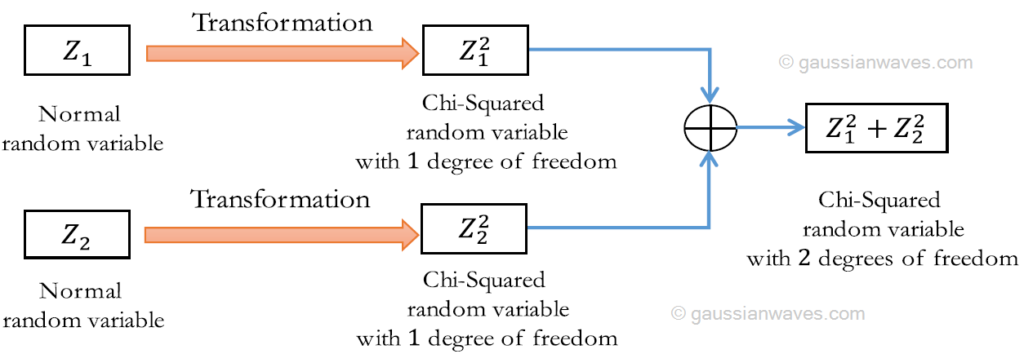
If \(Z\sim N(0,1)\) and \(U\sim \chi^2(r)\) are independent, then the random variable:įollows a \(t\)-distribution with \(r\) degrees of freedom. A chi-square random variable X with n degrees of freedom has probability density function f(x) xn/21ex/2 2n/2(n/2) x >0, for n 1,2.


 0 kommentar(er)
0 kommentar(er)
